Manuel investiga la “singularidad” matemática de las curvas

INVESTIGADORES OAXAQUEÑOS.

Manuel investiga la “singularidad” matemática de las curvas

NÉSTOR YURI

JAVIER TOLEDO FLORES

Si Chavela Vargas afirmaba que los mexicanos nacen en donde se les pega la gana, Manuel podría decir que los oaxaqueños también. Técnicamente no es oaxaqueño, pero de corazón lo es, lo disfruta y aprovecha el ambiente relajado de nuestra ciudad para desarrollar su investigación en el campo de las matemáticas algebraicas. Él es tapatío, de meritito Guadalajara.

“No fui un alumno brillante, pero considero que era buen estudiante, aunque un poco introvertido, jamás busqué ser el más popular del grupo”. Así llegó hasta la preparatoria en su ciudad natal, en donde tuvo sus primeras oportunidades de participar en las Olimpiadas de Matemáticas y abrir los ojos a algo que no les enseñan en la escuela: a pensar como matemático, es decir, a pensar de manera lógica y ordenada. “No se trata de memorizar fórmulas, se trata de saber plantear los problemas y averiguar como resolverlos… es todo un mundo de creatividad, es aprender a hacerse las preguntas correctas”.

Una vez decidido el camino a seguir se preguntó dónde debería realizar su sueño. Le recomendaron dos caminos: la UNAM o la Universidad de Guanajuato. Se decidió por esta última porque ahí podría obtener una beca, lo que le ayudaría a sostener sus gastos al tener que mudarse desde Guadalajara, pero lo determinante fue el modelo de estudios muy enfocado en las áreas que a él le interesaban y por el nivel tan alto que tienen los profesores que, en su mayoría, ya son investigadores de CIMAT, que es el Centro de Investigación en Matemáticas, una institución vinculada al Conahcyt y de muy alto nivel.

El ambiente de la Academia es muy demandante y provoca demasiado estrés, por ello mismo, Manuel decidió tomar un descanso para analizar qué haría al concluir su licenciatura. Finalmente tomó la decisión de continuar sus estudios y se matriculó en la UNAM para cursar su Maestría. Ahí trabajó en el área de geometría algebraica, la cual estudia objetos geométricos que pueden ser descritos a partir de ecuaciones algebraicas.

“En mi tesis de maestría trabajé con conjuntos de puntos en el plano. Por ejemplo, tres puntos distintos en el plano por lo general determinan un triángulo; pero uno puede considerar tres puntos alineados (colineales), de forma que el triángulo que definían desaparezca. En términos algebraicos, cuando los tres puntos se vuelven colineales aparece una nueva ecuación: la ecuación de la recta que los contiene. A grandes rasgos, éste es el tipo de fenómenos que estudié para conjuntos de más de tres puntos”.

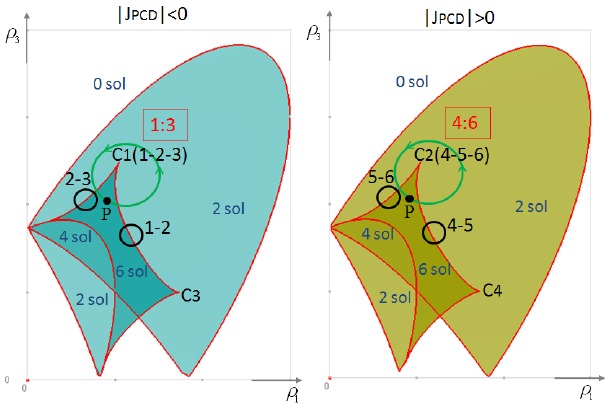
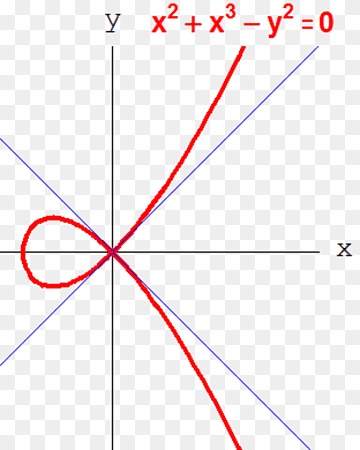
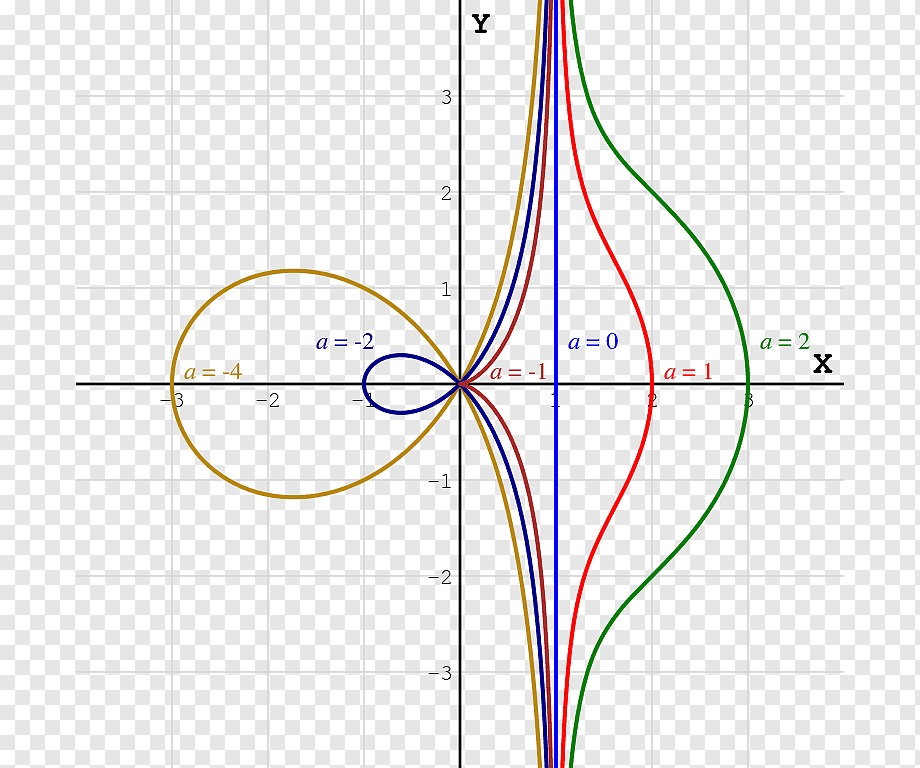
Para mi trabajo de Doctorado realizo estudios sobre curvas en el plano con «singularidades», es decir, puntos en los que la curva se interseca a sí misma. “Si uno empieza con una curva, es relativamente fácil encontrar sus puntos singulares. Lo que yo estoy buscando responder es la pregunta inversa: ¿De qué manera puedo reconstruir la curva si únicamente conozco sus puntos singulares?”. Entender estos conceptos matemáticos es complejo, pero en algún momento servirán para uso de los ingenieros en alguna aplicación práctica.

La geometría algebraica es una rama de las matemáticas que estudia las soluciones de sistemas de ecuaciones polinómicas. Combina métodos algebraicos y geométricos para comprender las propiedades geométricas de las soluciones de estos sistemas. En términos más simples, la geometría algebraica se centra en la intersección entre la geometría y el álgebra, analizando las propiedades geométricas de las soluciones de ecuaciones polinómicas utilizando herramientas algebraicas.

Las matemáticas algebraicas como otros campos de ellas son complejos y sus investigaciones normalmente les sirven a otros matemáticos, sin embargo, de manera sencilla, se puede decir que la geometría algebraica tiene numerosas aplicaciones en matemáticas puras y aplicadas, así como en campos como la física teórica, la criptografía y la teoría de códigos, entre otros.

“Para llegar a donde estoy lo que mas me ha ayudado es la determinación para lograr una meta. Admiro a todos aquellos que tienen el carácter para persistir en la búsqueda de algo, como, por ejemplo, quienes envían sus papeles a diferentes universidades las veces que sea necesario hasta lograr ser aceptados y nunca pierden el entusiasmo cuando sufren algún rechazo”.

Como a la mayoría de los jóvenes que están por concluir una carrera siempre existe la incertidumbre sobre su futuro. Manuel nos explica que ingresar a la Academia como investigador no es sencillo, pero es lo que a él le interesa, aunque con absoluta seguridad nos dice que, para alguien como él, el campo laboral es muy amplio: “Todo lo que es la industria, los bancos y las aseguradoras que manejan inversiones de riesgo, el sector de la computación o el de la inteligencia artificial por ejemplo”. Contrario a la idea que mucho podríamos tener, ser un matemático no quiere decir que forzosamente deba dedicarse a la docencia.

Normalmente asociamos a Oaxaca con la imagen de conflicto. Sin embargo, el trabajo de Manuel, sus compañeros y profesores nos dan otra imagen de lo que es nuestra tierra. Poca gente sabe del Instituto de Matemáticas de la UNAM en el corazón de nuestra ciudad, a un costado de la Alameda, detrás de los puestos de los vendedores triquis. Gracias a su trabajo y al de otros jóvenes en otros institutos del país México seguirá los pasos de naciones muy poderosas en esa área, como Singapur, Corea del Sur, Japón, China, Finlandia o Canadá.

Manuel Leal Camacho está a punto de Doctorarse en Matemáticas. Para él y todos los matemáticos una felicitación adelantada: el 14 de marzo es el Día Internacional de las Matemáticas porque es el día Pi, es decir, es el día 3/14.

Contacto: nestoryuri@yahoo.com